Lesson Plans For Kids That Like Cars
- Lachlan Palmer

- Feb 29, 2024
- 9 min read

Having a student that likes cars in a class can be... a little detrimental to a functioning class. How do we know? Well, we were once those exact kids. Couldn't focus on the work, constantly distracted by Jalopnik, Stanceworks or some other car news website, and god forbid we were sitting near a window if a cool car drove past.
See, here's the thing, a lot of us who were massively into cars, even as kids, are actually pretty capable of learning when presented with tools that accommodate our special interests.
Liking cars inherently comes with the want and need to understand some pretty complex theories, as well as to retain some pretty specific data.
For example, ask a kid that's into cars how much power and torque one of their favourite cars make and then see if they can describe what torque does. You might be surprised that they have at least a loose grip on the term newton metres just off the bat.
In fact, while a mechanics and car enthusiasts often have a pretty difficult time during school, you'd be surprised at the breadth of knowledge many of us take on just understanding how a car works.
Things like calorific content, forces, momentum, arithmetic, algebra, chemistry, plumbing, fabrication, manual arts, electrical, and (for someone like us) even a basic grip on English and Japanese. How else could we understand what random parts we're buying from a shady website for some clapped-out Honda from the 90's.
Now, the problem for many of us is that some teachers aren't willing to reach us on a level that we understand. This was our experience in school, but it seems similar for many of the enthusiasts and mechanics we talk to.
While plenty of assignments are asking to calculate the trajectory of a soccer ball, no one ever wants us to calculate the differing radii of a turn and how it relates to the optimal racing line.
So, here's some examples we came up for when asked recently.
Maths
Averages, percentages, fractions, ratios and decimals
This one is probably the easiest one to incorporate some sort of car-based learning into as there's so many potential uses for this. It also requires a little bit of an understanding of what these tools can be used for in the automotive world.
The easiest example we can come up with for averages include taking the power ratings of a particular manufacturer and finding the averages outputs. For example, if Ferrari makes 7 cars rated at 500hp, 600hp, 700hp, 700hp, 800hp, 900hp, and 1000hp, the find the mean, median and mode of the horsepower ratings.
From this, you can easily calculate fractions and percentages as well. For example, what percentage of the Ferrari's listed make over 700hp. Show this as a fraction and as a percentage.
This can also be translated into other areas that are a little more difficult to understand. If you wanted to give a student a real challenge, you can take the total race finishing times of the last Grand Prix and ask them to find the average race time.
This is particularly challenging as it involves the understanding of hours, minutes, seconds and milliseconds (or decimals). It you want to add a little spice to this, tell them that the race organisers have implemented a new rule where the last -place finisher must finish within 125% of the average race time and get them to calculate the maximum allowed time.
With all of that said, probably the most fun example you can work through with students is ratios. This is super easy with cars because almost every vehicle we can think of uses gearsets to reduce or increase the speed of the wheels compared to the engine.
Now, ratios make the most sense in the realm of off-road vehicles. For something like a GU Nissan Patrol (the big ugly mum bus you're probably picturing when you think of a 4WD), there is actually 3 sets of ratios going on at any one time. The gearbox, the transfer case and the differentials.
These all act together to change the output speed of the wheels. Our example goes a little something like this.
"A Nissan Patrol differential has a 63 tooth input gear and a 15 tooth output gear. What is the ratio for the differential?"
"The Nissan Patrol's engine is turning at 2000rpm (revolutions per minute), the transfer case ratio is 2.86:1 and the first gear ratio is 4.262:1. Taking the differential ratio you calculated above, what is the rpm of the tyre?"
"The diameter of the tyre is 35 inches (89cm) how many meters does the Nissan Patrol travel in 1 hour?"
Angles, degrees and Pythagoras
This one is going to be short as we haven't had much time to think about this, but let the students know that every cylinder must fire within every 2 rotations of the engine. Tell them a vehicle has 1, 2, 3, 4, 5, 6 or 8 cylinders and ask them to calculate the degrees between each firing of a cylinder.
You can add to this significantly by then giving them the firing order of these cylinders and asking them to draw and represent the separation on 2 circles. I this case, we recommend choosing an engine design with an odd number of cylinders like a Volvo 5 cylinder with the firing order 12453.
Another great example of how to use vehicles to teach angles it to look at the approach and departure angles of particular vehicles. This uses the Pythagoras theory to find what angle of slope a 4WD can approach or depart.
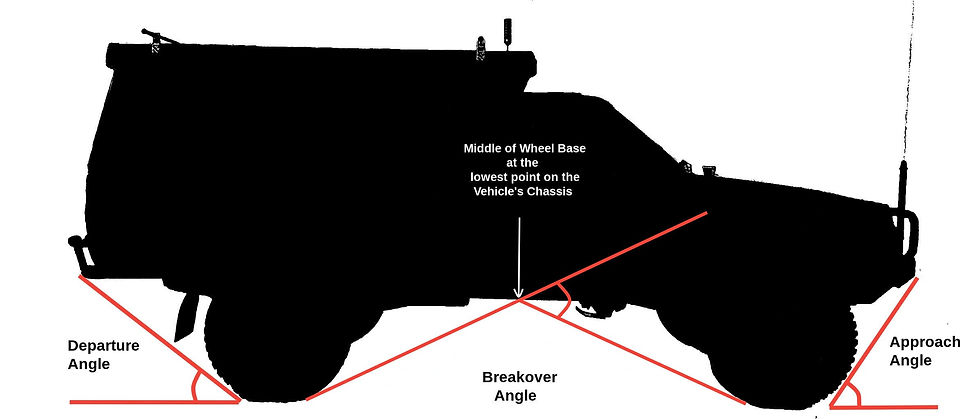
The best way to do this is to take a couple of different vehicles, like a Nissan Patrol, a Toyota Landcruiser and a Suzuki Jimny and give them the distance from the front wheel centre to the bottom of the front bumper and the height of the front bumper off of the ground.
By drawing a right-angle triangle using these numbers, you can then use the Pythagoras theory to calculate the angle on the leading edge of the tyre.
Area and volume
It is fairly simple to incorporate cars with the ideas of area and volume, but it is often overlooked mostly due to the fact that it requires a little extra effort.
Our favourite example of this actually relates to the useable cargo area of vehicles. For example, did you know that a tiny Japanese delivery truck and the current Ford F150 have roughly the same sized bed?
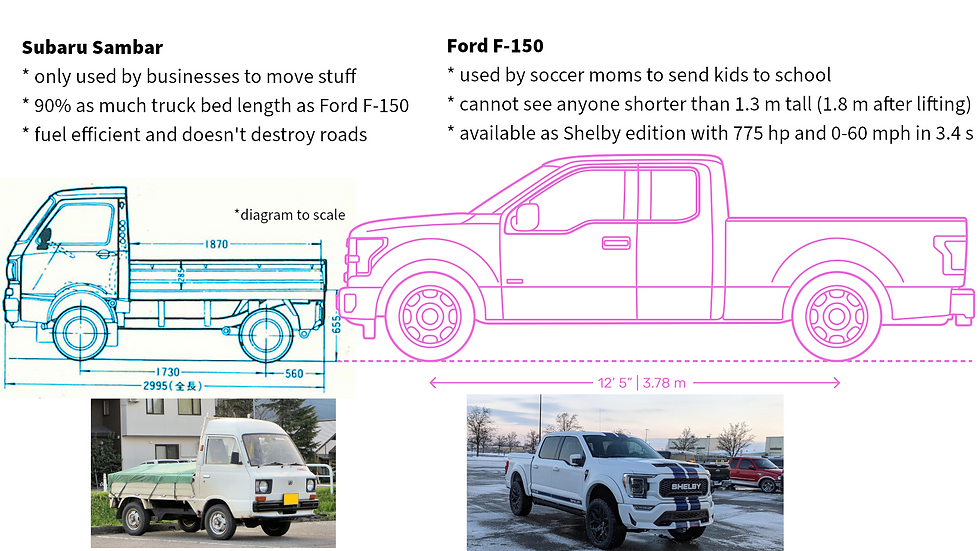
A good way to be include area for students that like cars is to ask them to calculate the total amount of area both vehicles take up on the road and then calculate the bed area. You could easily link this back to percentages by asking them to then calculate the percentage of each vehicle that is usable cargo space.
This is one of our favourites as it shows that 2 drastically different sized objects can still have the same usable area and the difference between internal and total area.
Volume is also quite a fun one to look at as a car enthusiast as you can give problems that basically equate to Tetris.
For the first one, have them calculate the internal volume of a moving truck. After this, give them the sizes of 5 different objects and ask them to calculate if they could theoretically fit inside the truck.
For bonus points, we would recommend making sure that one or more of these items are either too long or too tall to actually fit and asking the students if the items could fit and ask them to give the reason why.
The final part of teaching volume includes some engine displacements. This one is pretty difficult to understand but could be laid out a little something like this.
"A Hemi engine has a hemispherical combustion chamber at the top of the cylinder. The bore (diameter) is 10cm and the stroke (height) is 10cm. The hemisphere at the top of the cylinder is also 10cm in diameter. What is the volume of each cylinder?"
An add on to this would be, " A Hemi engine has 8 cylinders, what is the total volume of the engine?".
Algebra
We probably had to think about this one the hardest of all (because we haven't used it since high-school), but we think we've got some good ideas here.
In fact, this all goes back to the engine displacement we calculated before.
Take the KUN26R Toyota Hilux with it's 3L, 4 cylinder engine. A simple equation for this could be that the displacement (D) of the engine equals 4x the total volume (V) of each cylinder. Therefore D=4V and D/4=V.

Going a little deeper on this is also pretty simple. If you create a rule that total the cylinder volume is 3 times the size of the combustion chamber (C) plus 1, you can end up with a pretty interesting little equation to solve for C.
D=4V
D=4(3C+1)
D/4=3C+1
D/4-1=3C
(D/4-1)/3=C
(3000/4-1)/3=C
249.666=C
C=249.666
Now, more complex algebra is less common in the field of mechanics, but at least with a starting point, there is somewhere to go.
Science
Physics (forces and momentum)
Now, after all this writing, we're starting to get super tired. And your other students will also be weary of the car analogies by now, but that's on them.
Arguably, science was one of our favourite subjects when we were in school (besides manual arts) as it really lends itself to anything related to cars.
In fact, physics is one of the easiest ones to come up with automotive examples for as literally everything about forces can be applied to cars.
One thing to look at here is momentum.

"A Dodge Ram 1500 is a ghastly, overweight burden on society that weighs in at a shocking 2750kg. If it is travelling at 50km/h how many Ns of momentum does it have?"
This also works backwards.
"Another vehicle is travelling at 100km/h and has the same amount of momentum, what is its weight?".
Now, our example of how momentum turns into force is a bit grim, but there are tonnes of ways that you can do something similar that doesn't sound like a murder mystery.
"The Ram crashes into a tree. It goes from 50km/h to 0km/h in 5 seconds. What is the rate of deceleration?"
Try it out on them.
If they're still looking at you, mouth agape and drool slowly falling from their slack jaws, eye's glazed over while they play scratch and sniff with their armpits, let them know that newton meters how we measure a vehicle’s torque output.
Chemistry
Now, one of our favourite experiments involved understanding the calorific content of a given substance. In fact, to this day we still think about how interesting it is that every substance has an innate amount of energy available and that the way to measure that is with fire.
This is a little difficult to pull off in a class due to the highly volatile nature of certain fuels, however if you're doing an experiment like this in class you can have them guess the calorific content of methanol and petrol in compared to sugar.
Languages
English
We think that this is probably the most straight-up fun you can have with any child that's into cars as it allows them to show off their creativity in a good light. On top of this, there are so many great stories out there in the automotive world that lend themselves to creative writing.
If you didn't know, the man behind the Delorean Motor Company (the car from "Back To The Future") was involved in a crazy plot where they swindled millions of pounds from the Irish government, was charged with drug trafficking and that led to rumours that one of the most famous people in automotive history faked their own death.
In fact, there are so many different ways to include something automotive in an English class that it's hard to think of them all.
Have them write a review of their family car for magazine or opinion style writing.
When it comes to news, ask them to report on the racing results at the end of the Cars movie. Or to write an article about the Takata airbag recall and how big of a deal it is; Or give them parameters of a scientific breakthrough that will allow flying vehicles to exist and report on how they have affected traffic.
Better yet, ask them to report on any one of the multiple cheating scandals in racing over the last 40 years. This is a great one as it allows you to accommodate for all students by asking them to report on a scandal in an area they're interested in.
With all that said, the most entertaining type of writing will always be something creative. For this, we recommend a couple of things. For short stories, ask them to write about an off-road racing event held in a dystopian future.
Another option is the prompt "What would the world look like today if petrol powered engines didn't exist and steam was still prevalent?".
The options for including some sort of motoring theme in the English language is incredible and gives kids like us room to stretch our legs.
Japanese
We don't have too much to say here, as it's definitely not going to be useful for conversational Japanese. However, for reading exercises, the amount of Japanese written on the parts inside of a older Toyota, Honda or Nissan is truly shocking.
We started doing DuoLingo last year before a Japan trip and we're now getting to the point where a portion of the stickers on parts made in Japan make sense.
If cars and stickers are a little below the learning level and we're looking at really reading in Japanese, we recommend any car based manga. Initial D got us into cars in the first place and Over Rev is meant to cover similar topics with a focus on the females involved.
Conclusion
Here's the thing. We don't know anything about how to really teach kids. However, we do know that we were some of the most easily distracted and disruptive students in our classes and so many other car enthusiasts are just the same.
It's a little something you can do that show kids you care about their interests and that allows us to apply complex principles in a way that matters to us. Check out the links below for some more information.
If you have any questions about this blog post, would like a second opinion from a mechanic or would like to find an honest mechanic in Brisbane, check out Kashy here.




Comments